In celebration of the recent resolution of the Kadison-Singer problem by Marcus, Spielman, and Srivastava, here is a question on isotropic point sets on which Kadison-Singer does not (seem to) shed any light. A positive resolution would likely have strong implications for the Sparsest Cut problem and SDP hierarchies. The question arose in discussions with Shayan Oveis Gharan, Prasad Raghavendra, and David Steurer.
Open Question: Do there exist constants such that for any
, the following holds? Let
be a collection of
orthonormal bases and define
. Then there are subsets
with
and
.
[Some additional notes: One piece of intuition for why the question should have a positive resolution is that these orthonormal bases which together comprise at most
vectors cannot possibly “fill”
-dimensional space in a way that achieves
-dimensional isoperimetry. One would seem to need
points for this.
One can state an equivalent question in terms of vertex expansion. Say that a graph on
vertices is a vertex expander if
for all subsets
with
. Here,
denotes all the nodes that are in
or are adjacent to
. Then one can ask whether there exists a 1-1 mapping from
to
for some orthonormal bases
such that the endpoints of every edge are mapped at most
apart (as
).]
What would be the implication for sparsest cut?
Strictly speaking, there is no direct implication because this question is the “hard part” of a more general question. The more general question is to find such separated sets given any set of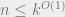 unit vectors in isotropic position.
unit vectors in isotropic position.
The implication is as follows: For every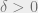 , there is a number
, there is a number 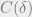 such that Sparsest Cut admits a
such that Sparsest Cut admits a 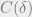 -approximation in time
-approximation in time 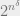 , i.e. sub-exponential time constant factor approximations to (uniform) Sparsest Cut.
, i.e. sub-exponential time constant factor approximations to (uniform) Sparsest Cut.
What is your precise definition of isotropic position? Is it that the covariance matrix (the sum of uu^T over vectors u in the set) is a multiple of the identity or is it exactly the identity? Seems like it’s the former, but just want to make sure.
More specifically, the general condition is as follows: Given unit vectors
unit vectors  , we assume that
, we assume that 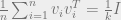 . Of course, a special case is when the vectors
. Of course, a special case is when the vectors  can be partitioned into orthonormal bases.
can be partitioned into orthonormal bases.
Is it important that the bases are over the reals? I think I can see a construction of such sets over complex vector spaces.
A general construction of such A,B over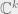 would be equally remarkable (and useful).
would be equally remarkable (and useful).
Wow, awesome blog layout! How long have you been blogging
for? you made blogging look easy. The overall look of your web site is wonderful, as well as the
content!