What does Kadison-Singer have to do with Quantum Mechanics?

Most accounts of the Kadison-Singer problem mention that it arose from considerations in the foundations of quantum mechanics. Specifically, a question about “extensions of pure states.” See, for instance, Gil’s blog. But trying to reconcile this question with my (limited) knowledge of QM proved frustrating. There is also an intuitive explanation posted at soulphysics, along with mathematical notes. But I couldn’t figure that one out either, because it only deals with “normal” quantum states (those corresponding to countably additive measures; see below). I think the KS problem for normal states is trivial. For the meat of KS, one has to think not only about infinite-dimensional spaces, but about “pathological” (non-constructible) measures. In particular, one has to think about “quantum states” that don’t have density matrices.

What follows are my notes on the matter, all of which are either well-known or wrong. Skip to the end for the very simple formulation with no mention of quantum states. Even better advice is to just Read Nick Harvey’s survey.

How I understand quantum measurement

A (mixed) quantum state ${\rho}$ on the space ${\mathbb C^n}$ is an ${n \times n}$ Hermatian matrix satisfying ${\rho \succeq 0}$ ( ${\rho}$ is positive semi-definite) and ${\mathrm{Tr}(\rho)=1}$ . Suppose we also have a resolution of the identity: A collection ${\mathcal M = \{M_1, M_2, \ldots, M_k\}}$ of PSD matrices with ${\sum_{j=1}^k M_j = I}$ . Then when we perform the measurement ${\mathcal M}$ , the probability of obtaining outcome ${j}$ is ${\mathrm{Tr}(\rho M_j)}$ for ${j=1,2,\ldots,k}$ .

A pure state is given by a density matrix of the form ${\rho = \psi \psi^T}$ for some ${\psi \in \mathbb C^n}$ . Equivalently, a state is pure if and only if it cannot be written as a non-trivial convex combination of other states, i.e. if ${\rho = \lambda \rho_1 + (1-\lambda) \rho_2}$ for ${\lambda \in (0,1)}$ , then ${\rho=\rho_1=\rho_2}$ . The pure states are the extreme points of the convex set of all states.

Quantum logic

There is another way to think about quantum measurement. Let ${\mathcal H}$ be a (separable) Hilbert space and consider a projection ${P : \mathcal H \rightarrow S}$ onto some closed subspace. A measure ${\mu}$ on projections assigns to every such projection a value in ${[0,1]}$ . We say that ${\mu}$ is ${\sigma}$ -additive if whenever ${Q = \sum_{j=1}^{\infty} P_j}$ and the projections ${\{P_j\}}$ are mutually orthogonal, we have ${\mu(Q) = \sum_{j=1}^{\infty} \mu(P_j)}$ . If this only holds for finite sums of projections, we say that ${\mu}$ is finitely additive. We should also have ${\mu(I)=1}$ .

Note that we have allowed here the possibility that ${\mathcal H}$ is infinite-dimensional. In the case where the measure ${\mu}$ is ${\sigma}$ -additive, it is completely specified by its value at one-dimensional projections, i.e. the values ${\mu(P_x)}$ where ${P_x}$ denotes projection onto ${x \in \mathcal H}$ . Now we can state Gleason’s theorem: Our two notions of quantum measurement coincide.

Theorem 1 Let ${\mathcal H}$ be a Hilbert space of dimension at least 3 and let ${\mu}$ be a ${\sigma}$ -additive measure on projections. Then there exists a unique linear operator ${\rho}$ such that for any projection ${P}$ , we have ${\mu(P) = \mathrm{Tr}(\rho P)}$ .

In other words, every ${\sigma}$ -additive measure on projections arises from a mixed state.

Restricted purity

Note that a measure on projections corresponds to a pure state if and only if it cannot be written as a non-trivial convex combination of measures on projections. In this way, we can also define purity with respect to a restricted family of projections.

Consider, for example, the Hilbert space ${\ell^2(\mathbb N)}$ of complex sequences, and let ${\{e_j : j \in \mathbb N\}}$ denote the standard basis. Suppose we consider only the projections ${\mathcal P = \{P_j\}}$ onto each of the basis elements. Say that a ${\mathcal P}$ -measure is a measure on all projections of the form ${\sum_{i \in A} P_i}$ for ${A \subseteq \mathbb N}$ . Such a measure only gives us probabilities for measurements performed in the standard basis. (The algebra generated by ${\mathcal P}$ is a canonical example of a “maximal abelian subalgebra,” i.e. MASA.) We can say that a ${\mathcal P}$ -measure is pure if it cannot be written as a non-trivial convex combination of other ${\mathcal P}$ -measures. What are the pure ${\mathcal P}$ -measures? Well, the only ${\sigma}$ -additive pure ${\mathcal P}$ -measures are the point measures ${\mu(P_j)=1}$ for some ${j}$ . If ${\mu(P_j), \mu(P_{j'}) > 0}$ for ${j \neq j'}$ , then by ${\sigma}$ -additivity, we can split ${\mu}$ into a convex combination of two measures (one supported only on ${P_j}$ and the other supported off ${P_j}$ ).

But when ${\sigma}$ -additivity is dropped, some tricky things can happen (see the next section). It turns out that, in this case, there are more pure states than just ${e_j e_j^T}$ (in fact, the cardinality of the finitely-additive pure states is gigantic, ${2^{2^{\aleph_0}}}$ ). Now we are in position to state the Kadison-Singer problem.

Kadison-Singer Problem: Is it the case that every pure, finitely-additive ${\mathcal P}$ -measure has a unique extension to a finitely-additive measure on all the projections of ${\mathcal H}$ ?

The answer is clearly positive for ${\sigma}$ -additive measures (in which case the unique extension corresponds to ${e_j e_j^T}$ ). The answer is also positive for finitely-additive ${\mathcal P}$ -measures, as recently proved by Marcus, Spielman, and Srivistava.

In their original work, Kadison and Singer showed that the answer is false if one constructs the MASA using the continuous Hilbert space ${L^2([0,1])}$ instead of ${\ell^2(\mathbb N)}$ . One can take the subalgebra ${\mathcal C}$ of multiplication operators ${T_g (f)=gf}$ for ${\|g\|_{\infty} < \infty}$ . Here the corresponding family of projections are the maps ${P_S f = \mathbf{1}_S f}$ for ${S \subseteq [0,1]}$ . Unlike in the case above, this subalgebra is not “discrete.” It turns out that every maximal abelian subalgebra of bounded operators on a separable Hilbert space is either finite-dimensional, the discrete one, the continuous one, or a direct sum of algebras isomorphic to these.

Note that states corresponding to finitely additive (but not ${\sigma}$ -additive measures) do not have density matrices and are often considered to be “unphysical” because they would take an infinite amount of energy to prepare.

A ${\beta}$ -world teeming with pure states

In the above setting, we said there are finitely-additive pure ${\mathcal P}$ -measures ${\mu}$ other than point measures. To see what one of these must look like, consider the following construction. Let ${P_{\mathrm{even}}}$ denote the projection onto ${\{e_j : j \textrm{ even}\}}$ and define ${P_{\mathrm{odd}}}$ similarly. Define the measures ${\mu_{\mathrm{even}}(P) = \mu(P P_{\mathrm{even}})}$ and ${\mu_{\mathrm{odd}}(P) = \mu(P P_{\mathrm{odd}})}$ . Then we can write ${\mu = \mu(P_{\mathrm{even}}) \mu_{\mathrm{even}} + \mu(P_{\mathrm{odd}}) \mu_{\mathrm{odd}}}$ . This is a non-trivial convex combination unless either ${\mu(P_{\mathrm{even}})=0}$ or ${\mu(P_{\mathrm{odd}})=0}$ .

Indeed, for every partition ${\mathbb N = S \cup \bar S}$ , a pure ${\mathcal P}$ -measure ${\mu}$ can only put non-zero weight on projections involving coordinates of exactly one of ${S}$ or ${\bar S}$ . Furthermore, if ${\mu(\sum_{i \in {\bar S}} P_i) = 0}$ then ${\mu(\sum_{i \in S} P_i)=1}$ . In other words, for every set of projections, the measure ${\mu}$ takes only values 0 or 1. Such finitely-additive measures are exactly given by ultrafilters on ${\mathbb N}$ . The finitely-additive pure ${\mathcal P}$ -measures are in one-to-one correspondence with such ultrafilters, the set of which can be identified with ${\beta \mathbb N}$ , the Stone-Cech compactification of the naturals. See Terry Tao’s notes on ultafilters and Stone-Cech compactification.

A simple formulation

Take the Hilbert space ${\ell^2 = \ell^2(\mathbb N)}$ with standard basis ${\{e_j : j \in \mathbb N\}}$ , and let ${\mathcal S}$ denote the set of all its closed subspaces. Consider a map ${\mu : \mathcal S \rightarrow [0,1]}$ . We say that ${\mu}$ is a finitely-additive measure if ${\mu(\ell^2)=1}$ and whenever ${S_1, S_2, \ldots, S_k \in \mathcal S}$ is a finite collection of mutually orthogonal subspaces, we have ${\mu(\mathrm{span}(S_1, \ldots, S_k)) = \sum_{i=1}^k \mu(S_i)}$ . Say that such a measure ${\mu}$ is pure if it cannot be written as a non-trivial convex combination of two finitely-additive measures. A canonical example of a pure measure involves fixing a unit vector ${x \in \ell^2}$ and setting ${\mu(S) = \langle x, P_S x\rangle}$ where $P_S$ denotes the orthogonal projection onto $S$ .

Now let ${\mathcal S_{\mathrm{diag}}}$ be the set of all the subspaces of ${\ell^2}$ of the form ${\mathrm{span}(e_i : i \in A)}$ for some subset ${A \subseteq \mathbb N}$ , i.e. all the coordinate subspaces. We can define “finitely-additive” and “pure” for measures on ${\mathcal S_{\mathrm{diag}}}$ in the analogous way.

Kadison-Singer problem: Can every finitely-additive pure measure on ${\mathcal S_{\mathrm{diag}}}$ be extended uniquely to a finitely-additive measure on ${\mathcal S}$ ?

Note that the real question is about uniqueness of the extension. There always exists a pure extension; see the comments.

6 thoughts on “What does Kadison-Singer have to do with Quantum Mechanics?”

David R. MacIver says:

July 30, 2013 at 1:04 am

Am I missing something or is your canonical example of a pure measure never finitely additive? If we take two orthogonal vectors u and v such that x = u + v then mu(span(u)) = mu(span(v)) = 0 but mu(span(u, v)) = 1.
James Lee says:

July 30, 2013 at 1:35 am

Yeah, you’re right. What I wrote didn’t make any sense at all. I changed the text to what I had intended.
drmaciver says:

July 30, 2013 at 6:27 am

I think a similar problem also breaks your canonical pure extension: Let u = e_1 + e_2 and v = e_1 – e_2. Then mu^(span(u)) = mu^(span(v)) = 0 because there are no basis vectors in there, but mu^(span(u, v)) = mu^(span(e_1, e_2)) = mu(span(e_1, e_2)) which is not necessarily zero.
James Lee says:

July 30, 2013 at 4:46 pm

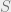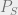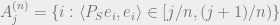Agreed. I think an attempt to do it correctly actually reveals the relationship to “paving conjectures.” Let $\mu$ be a pure measure on $\mathcal S_{\mathrm{diag}}$ . Consider a subspace $S$ and and the associated orthogonal projection $P_S$ . Also take a partition of the interval $[0,1] = \bigcup_{j=0}^{n-1} [j/n, (j+1)/n)$ . Let $A^{(n)}_j = \{ i : \langle P_S e_i, e_i \rangle \in [j/n, (j+1)/n)\}$ . Finally, define
$\displaystyle \hat \mu(S) = \lim_{n \to \infty} \sum_{j=0}^{n-1} \mu\left(\vphantom{\bigoplus}\mathrm{span}(e_i : i \in A^{(n)}_j)\right) \frac{j}{n}$ .
By properties of ultrafilters, for every n, the sum inside the limit only has one non-zero term.

In other words, $\hat \mu(S) = \lim_{\mathcal U} \langle e_i, P_S e_i\rangle$ where $\mathcal U$ is the ultrafilter defining $\mu$ .
Pingback: The Kadison-Singer Conjecture has beed Proved by Adam Marcus, Dan Spielman, and Nikhil Srivastava | Combinatorics and more
math-children says:

January 8, 2014 at 7:28 am

Good article