Majorizing measures

~ James

At STOC 2010 last week, Talagrand gave a presentation on some of his favorite open problems, which included a quick review of Gaussian processes and the majorizing measures theory. In joint work with Jian Ding and Yuval Peres, we recently showed how the cover time of graphs can be characterized by majorizing measures.

While I’ll eventually try to give an overview of this connection, I first wanted to discuss how majorizing measures are used to control Gaussian processes. In the next few posts, I’ll attempt to give an idea of how this works. I have very little new to offer over what Talagrand has already written; in particular, I will be borrowing quite heavily from Talagrand’s book (which you might read instead).

Gaussian processes

Consider a Gaussian process {\{X_t\}_{t \in T}} for some index set {T} . This is a collection of jointly Gaussian random variables, meaning that every finite linear combination of the variables has a Gaussian distribution. We will additionally assume that the process is centered, i.e. {\mathbb E(X_t) = 0} for all {t \in T} .

It is well-known that such a process is completely characterized by the covariances {\{\mathop{\mathbb E}(X_s X_t)\}_{s,t \in T}} . For {s,t \in T} , consider the canonical distance,

\displaystyle d(s,t) = \sqrt{\mathbb E\,|X_s-X_t|^2},

which forms a metric on {T} . (Strictly speaking, this is only a pseudometric since possibly {d(s,t)=0} even though {X_s} and {X_t} are distinct random variables, but we’ll ignore this.) Since the process is centered, it is completely specified by the distance {d(s,t)} , up to translation by a Gaussian (e.g. the process {\{X_t + X_{t_0}\}_{t \in T}} will induce the same distance for any {t_0 \in T} ).

A concrete perspective

If the index set {T} is countable, one can describe every such process in the following way. Let {\{g_i\}_{i=1}^{\infty}} be a sequence of i.i.d. standard Gaussians, let {T \subseteq \ell^2} , and put

\displaystyle X_t = \sum_{i \geq 1} g_i t_i.

In this case, it is easy to check that {d(s,t) = \|s-t\|_2} for {s,t \in T} . (That this construction is universal follows from the fact that every two separable Hilbert spaces are isomorphic.)

Random projections

If {T} is finite, then we can think of {T \subseteq \mathbb R^n} for some {n \in \mathbb N} . In this case, if {g} is a standard {n} -dimensional Gaussian, then

\displaystyle X_t = \langle g, t \rangle,

and we can envision the process as the projection of {T} onto a uniformly random direction.

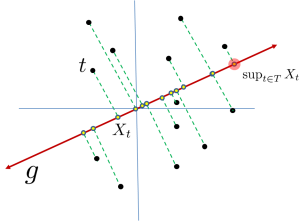
Studying the maxima

We will be concerned primarily with the value,

\displaystyle \mathbb E \sup_{t \in T} X_t.

(I.e. the expected value of the extremal node circled above.) One may assume that {T} is finite without losing any essential ingredient of the theory, in which case the supremum can be replaced by a maximum. Note that we are studying the tails of the process. Dealing with these extremal values is what makes understanding the above quantity somewhat difficult.

As some motivation for the classical study of this quantity, one has the following.

Theorem 1 For a separable Gaussian process {\{X_t\}_{t \in T}} , the following two assertions are equivalent.

  1. The map {t \mapsto X_t(\omega)} is uniformly continuous (as a map from {(T,d)} to {\mathbb R)} with probability one.
  2. As {\varepsilon \rightarrow 0} ,

    \displaystyle \mathop{\mathbb E}\sup_{d(s,t) \leq \varepsilon} |X_s-X_t| \rightarrow 0.

However, from our viewpoint, the quantitative study of {\mathbb E\sup_{t \in T} X_t} in terms of the geometry of {(T,d)} will play the fundamental role.

Bounding the sup

We will concentrate first on finding good upper bounds for {\mathop{\mathbb E}\sup_{t \in T} X_t} . Toward this end, fix some {t_0 \in T} , and observe that

\displaystyle \mathop{\mathbb E}\sup_{t \in T} X_t = \mathop{\mathbb E}\sup_{t \in T} (X_t - X_{t_0}).

Since {\sup_{t \in T} (X_t - X_{t_0})} is a non-negative random variable, we can write

\displaystyle \mathop{\mathbb E} \sup_{t \in T} (X_t - X_{t_0}) = \int_{0}^{\infty} \mathop{\mathbb P}\left(\sup_{t \in T} X_t - X_{t_0} > u\right)\,du,

and concentrate on finding upper bounds on the latter probabilities.

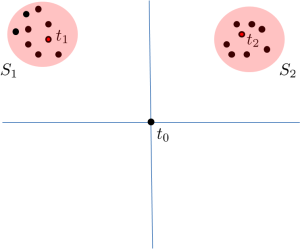
Improving the union bound

As a first step, we might write

\displaystyle \mathop{\mathbb P}\left(\sup_{t \in T} X_t - X_{t_0} > u\right) \leq \sum_{t \in T} \mathop{\mathbb P}\left(X_t - X_{t_0} > u\right).

While this bound is decent if the variables {\{X_t-X_{t_0}\}_{t \in T}} are somewhat independent, it is rather abysmal if the variables are clustered.

Since the variables in, e.g. {S_1} , are highly correlated (in the “geometric” language, they tend to project close together on a randomly chosen direction), the union bound is overkill. It is natural to choose representatives {t_1 \in S_1} and {t_2 \in S_2} . We can first bound {X_{t_1}-X_{t_0}} and {X_{t_2}-X_{t_0}} , and then bound the intra-cluster values {\{X_t - X_{t_1}\}_{t \in S_1}} and {\{X_t - X_{t_2}\}_{t \in S_2}} . This should yield better bounds as the diameter of {S_1} and {S_2} are hopefully significantly smaller than the diameter of {T} .

Formally, we have

\displaystyle \mathop{\mathbb P}\left(\sup_{t \in T} X_t - X_{t_0} > u\right) \leq

\displaystyle \mathop{\mathbb P}(X_{t_1} - X_{t_0} > u/2) + \sum_{t \in S_1} \mathop{\mathbb P}(X_t - X_{t_1} > u/2)

\displaystyle + \mathop{\mathbb P}(X_{t_2} - X_{t_0} > u/2) + \sum_{t \in S_2} \mathop{\mathbb P}(X_t - X_{t_2} > u/2).

Of course, there is no reason to stop at one level of clustering, and there is no reason that we should split the contribution {u = u/2 + u/2} evenly. In the next post, we’ll see the “generic chaining” method which generalizes and formalizes our intuition about improving the union bound. In particular, we’ll show that every hierarchical clustering of our points offers some upper bound on \mathbb E \sup_{t \in T} X_t .

3 thoughts on “Majorizing measures”

  1. Pingback: Gaussian Processes in Theory « Healthy Algorithms

Leave a comment