Kernels of random sign matrices

In the last post, we began proving that a random $N/2 \times N$ sign matrix $A$ almost surely satisfies $\Delta(\mathrm{ker}(A)) = O(1)$ . In other words, almost surely for every $x \in \mathrm{ker}(A)$ , we have

$\displaystyle \frac{\sqrt{N}}{O(1)} \|x\|_2 \leq \|x\|_1 \leq \sqrt{N} \|x\|_2.$

The proof follows roughly the lines of the proof that a uniformly random $N/2 \times N$ matrix $B$ with $\{0,1\}$ entries is almost surely the check matrix of a good linear code over $\mathbb F_2$ . In other words, with high probability, there does not exist a non-zero vector $x \in \mathbb F_2^N$ with hamming weight $o(N)$ , and which satisfies $Bx=0$ (this equation is considered over $\mathbb F_2$ ). The proof of this is simple: Let $B_1, B_2, \ldots, B_{N/2}$ be the rows of $B$ . If $x \neq 0$ , then $\Pr[\langle B_i, x \rangle = 0] \leq \frac12.$ Therefore, for any non-zero $x$ , we have

$\Pr[Bx = 0] \leq 2^{-N/2}.$ (**)

On the other hand, for $\delta > 0$ small enough, there are fewer than $2^{N/2}$ non-zero vectors of hamming weight at most $\delta N$ , so a union bound finishes the argument.

The proof that $\Delta(\mathrm{ker}(A)) = O(1)$ proceeds along similar lines, except that we can no longer take a naive union bound since there are now infinitely many “bad” vectors. Of course the solution is to take a sufficiently fine discretization of the set of bad vectors. This proceeds in three steps:

If $\|Ax\|_2$ is large, and $x$ is close to $x'$ , then $\|Ax'\|_2$ is also large.
Any fixed vector $x \in \mathbb R^N$ with $\|x\|_2 = 1$ has $\|Ax\|_2$ large with high probability. This is the analog of (**) in the coding setting.
There exists a small set of vectors that well-approximates the set of bad vectors.

Combining (1), (2), and (3) we will conclude that every bad vector $x$ has $\|Ax\|_2$ large (and, in particular, $x$ is not contained in the kernel).

To verify (1), we need to show that almost surely the operator norm $\|A\| = \max \left\{ \|Ax\|_2 : \|x\|_2 = 1\right\}$ is small.

From the last post, we have the following two statements.

Lemma 1: If $v \in \mathbb R^k$ and $X \in \{-1,1\}^k$ is chosen uniformly at random, then

$\displaystyle \Pr\left[|\langle v, X \rangle| \geq t\right] \leq 2 \exp\left(\frac{-t^2}{2 \|v\|_2^2}\right)$

The next theorem (see the proof from the last post) verifies (1) above.

Theorem 1: If $A$ is a random $N/2 \times N$ sign matrix, then

$\Pr[\|A\| \geq 10 \sqrt{N}] \leq 2 e^{-6N}$ .

Now we turn to proving (2), which is the analog of (**). We need to upper bound the small ball probability, i.e. the probability that $Av$ falls into a small ball (around 0) for any fixed $v \in \mathbb R^N$ . To start, we would like to say that for some fixed $v\in \mathbb R^N$ with $\|v\|_2 = 1$ , and a uniformly random sign vector $X \in \{-1,1\}^N$ , we have for example,

$\Pr[ |\sum_{i=1}^N X_i v_i| > 0.01] \geq 0.01$

These kinds of estimates fall under the name of Littlewood-Offord type problems; see the work of Tao and Vu and of Rudelson and Vershynin for a detailed study of such random sums, and the beautiful connections with additive combinatorics. For the above estimate, we will need only the simple Paley-Zygmund inequality:

Lemma 2: If $Z$ is a non-negative random variable and $0 < t < 1$ , then

$\displaystyle \Pr[Z \geq t (\mathbb EZ)] \geq (1-t)^2 \frac{(\mathbb EZ)^2}{\mathbb E(Z^2)}$

Proof: By Cauchy-Schwarz,

$\mathbb EZ = \mathbb E[Z\mathbf{1}_{\{Z < t (\mathbb EZ)\}}] + \mathbb E[Z\mathbf{1}_{\{Z \geq t(\mathbb EZ)\}}] \leq t \mathbb E[Z] + \sqrt{\mathbb E[Z^2]} \sqrt{\mathbb E[\mathbf{1}_{\{Z \geq t (\mathbb EZ)\}}]}$

Now observe that $\mathbb E[\mathbf{1}_{\{Z \geq t (\mathbb EZ)\}}] = \Pr[Z \geq t(\mathbb EZ)]$ and rearrange.

We can use this to prove our estimate on random sums.

Lemma 3: For any $v \in \mathbb R^N$ , if $X \in \{-1,1\}^N$ is chosen uniformly at random, then for every $0 < t < 1$ ,

$\displaystyle \Pr\left[|\langle X,v\rangle|^2 \geq t \|v\|_2^2 \right] \geq \frac{(1-t)^2}{12}.$

Proof: Apply Lemma 2 with $Z = |\langle X,v\rangle|^2$ . Note that by independence, we have $\mathbb E[Z] = \|v\|_2^2$ . Furthermore, for any non-negative random variable $Y$ and $0 < p < \infty$ , we have $\mathbb E[Y^p] = p \int_{0}^{\infty} \lambda^{p-1} \Pr(Y > \lambda)\,d\lambda$ , thus

$\displaystyle \mathbb E[Z^2] = \mathbb E[|\langle X,v\rangle|^4] = 4 \int_{0}^{\infty} \lambda^3 \Pr(|\langle X,v\rangle| > \lambda)\,d\lambda \leq 4\int_0^{\infty} \lambda^3 e^{-\lambda^2/(2\|v\|_2^2)}\,d\lambda,$

where the final inequality follows from Lemma 1. It is easy to see that the final bound is at most $12 \cdot \|v\|_2^4 = 12 (\mathbb EZ)^2$ .

Observing that $\|Av\|_2^2 = \sum_{i=1}^{N/2} |\langle A_i, v\rangle|^2$ , where $A_1, A_2, \ldots, A_{N/2}$ are the rows of $A$ yields:

Corollary 1: For any $v \in \mathbb R^N$ ,

$\displaystyle \Pr\left[\vphantom{\bigoplus} \|A v\|_2 \leq \frac{\sqrt{N}}{20} \|v\|_2\right] \leq e^{-N/100}.$

Proof: Apply Lemma 3 with $t = 1/16$ , say, and then use a Chernoff bound to show that the conclusion of the Lemma holds for a constant fraction of the trials $A_1, \ldots, A_{N/2}$ with overwhelming probability.

Using Theorem 1 and Corollary 1, we can verify (2):

Theorem 2: For any $v \in \mathbb R^N$ , we have

$\displaystyle \Pr\left[\mathrm{dist}(v, \mathrm{ker}(A)) \leq \frac{\|v\|_2}{200}\right] \leq 3 e^{-N/100}.$

Proof: By Theorem 1 and Corollary 1, we may assume that $\|A\| \leq 10 \sqrt{N}$ and $\|Av\|_2 \geq \frac{\sqrt{N}}{20} \|v\|_2$ . Let $x \in \mathrm{ker}(A)$ be the closest point to $v$ . Then $Ax = 0$ , so

$\|A(v-x)\|_2 = \|Av\|_2 \geq \frac{\sqrt{N}}{20} \|v\|2$ .

But since $\|A\| \leq 10\sqrt{N}$ , we must have $\|v-x\|_2 \geq \|v\|_2/200$ .

Let $B_{\ell_1}$ and $B_{\ell_2}$ be the unit balls of the $\ell_1$ and $\ell_2$ norms, respectively, in $\mathbb R^N$ . Property (3) above follows from the well-known fact that $\delta \sqrt{N} B_{\ell_1}$ can be covered by at most $(1600)^{\delta N}$ copies of $\frac{1}{400} B_{\ell_2}$ (see, e.g. Pisier’s book). We use this to finish the proof.

Theorem 3: There exists a constant $C \geq 1$ such that almost surely the following holds. Every $x \in \mathrm{ker}(A)$ satisfies

$\displaystyle \frac{\sqrt{N}}{C} \|x\|_2 \leq \|x\|_1 \leq \sqrt{N} \|x\|_2.$

In other words, $\Delta(\mathrm{ker}(A)) = O(1)$ .

Proof: Choose $\delta$ small enough so that $k = (1600)^{\delta N} < \frac13 e^{N/100}$ , and let $v_1, v_2, \ldots, v_k \in \mathbb R^N$ be such that

$\displaystyle \bigcup_{i=1}^k B_{\ell_2}(v_i, \tfrac{1}{400}) \supseteq \delta \sqrt{N} B_{\ell_1}$ .

By a union bound, we can assume that $\|A\| \leq 10 \sqrt{N}$ , and for every $i = 1, 2, \ldots k$ ,

$\mathrm{dist}(v_i, \mathrm{ker}(A)) \geq \frac{1}{200} \|v_i\|_2\quad(4)$

Now suppose there exists an $x \in \mathrm{ker}(A)$ with $\frac{\sqrt{N} \|x\|_2}{\|x\|_1} \geq C$ . We may assume that $\|x\|_1 = \delta \sqrt{N}$ and $\|x\|_2 = \delta C$ . But then $x \in \delta \sqrt{N} B_{\ell_1}$ , hence there exists a $v_i$ such that $\|v_i-x\|_2 \leq \frac{1}{400}$ . It follows that

$\|v_i\|_2 \geq \|x\|_2 - \|v_i-x\|_2 \geq \delta C - \frac{1}{400}.$

Choosing $C = 1/\delta$ , we have $\|v_i\|_2 > \frac12$ . But then (4) implies $\mathrm{dist}(v_i, \mathrm{ker}(A)) > \frac{1}{400}$ , contradicting $\|v_i-x\|_2 \leq \frac{1}{400}$ .

In the next post, we’ll see how such subspaces are related to error-correcting codes over the reals.

4 thoughts on “Kernels of random sign matrices”

aravind srinivasan says:

May 13, 2008 at 10:56 am

just a minor comment — in Lemma 2, all you need is that EZ >= 0, not that Z is non-negative necessarily; you can apply the Chebyshev-Cantellin inequality then (which will also lead to a slightly smaller denominator, but maybe Paley-Zygmund also leads to it).
Boaz Barak says:

June 12, 2008 at 6:07 am

Hi James,

Just came across this collection – it’s really nice. I hope you do keep up posting these. This is the kind of blog that’s actually worth reading.

I’m not sure I follow
dist(x’, ker(A)) >= dist(x,ker(A)) – |A||x-x’|
but it doesn’t matter much.

It seems that the equation you need (and use) is that
|x-x’| >= |A(x-x’)|/|A|

BTW I saw in your (great) powerpoint slides that you mentioned something that Milman conjectures is impossible. I hope you expand on that, and whether he conjectures an information theoretic lower bound, or that it’s hard to come up with an explicit construciton.

Boaz
jrluw says:

June 12, 2008 at 11:15 am

Boaz, thanks; you are right that the line

dist(x’, ker(A)) >= dist(x,ker(A)) – |A||x-x’|

doesn’t make any sense, and also that the proof doesn’t use it. I have changed the description of steps (1)-(3) to reflect what actually goes on in the proof.

About Milman’s “conjecture” — it was made informally at a talk he gave last year; I believe he intended to guess that there is no completely explicit construction, but it’s not clear what that means. E.g. he would not be happy with an arbitrary deterministic polynomial time algorithm. Note that no one knows how to compute $\Delta(X)$ efficiently. In fact, no one knows whether $\Delta(X) \geq C$ ? is in NP, or even how to give witnesses for $\Delta(X) \approx \sqrt{N}$ . 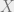Or even how to generate random $X$ ‘s that have a witness with high probability.
tasos says:

April 14, 2009 at 11:46 am

James, you forgot a sqrt(N) in the statement of theorem 3.