Open question: Cover times and the Gaussian free field

Here are a few fascinating open questions coming from my work with Jian Ding and Yuval Peres on cover times of graphs and the Gaussian free field. (Also, here are my slides for the corresponding talk.)

1. Cover times and the Gaussian free field

Consider a finite, connected graph ${G=(V,E)}$ and the simple random walk on ${G}$ (which, at every step, moves from a vertex to a uniformly random neighbor). If we let ${\tau_{\mathrm{cov}}}$ denote the first (random) time at which every vertex of ${G}$ has been visited, and we use ${\mathop{\mathbb E}_v}$ to denote expectation over the random walk started at ${v \in V}$ , then the cover time of ${G}$ is defined by

$\displaystyle t_{\mathrm{cov}}(G) = \max_{v \in V} \mathop{\mathbb E}_v \tau_{\mathrm{cov}}.$

On the other hand, consider the following Gaussian process ${\{g_v\}_{v \in V}}$ , called the (discrete) Gaussian free field (GFF) on ${G}$ . Such a process is specified uniquely by its covariance structure. Fix some ${v_0 \in V}$ , and put ${g_{v_0}=0}$ . Then the rest of the structure is specified by the relation

$\displaystyle \mathop{\mathbb E}(g_u-g_v)^2 = R_{\mathrm{eff}}(u,v)$

for all ${u,v \in V}$ , where ${R_{\mathrm{eff}}(u,v)}$ the effective resistance between ${u}$ and ${v}$ when ${G}$ is thought of as an electrical network. Equivalently, the density of ${\{g_v\}_{v \in V}}$ is proportional to

$\displaystyle \exp\left(-\frac12 \sum_{u \sim v} (g_u-g_v)^2\right),$

where the sum is over edges of $G$ .
One of our main theorems can be stated as follows.

Theorem 1 (Ding-L-Peres) For every graph ${G=(V,E)}$ , one has

$\displaystyle t_{\mathrm{cov}}(G) \asymp |E| \left(\mathop{\mathbb E} \max_{v \in V} g_v\right)^2,$

where ${\{g_v\}_{v \in V}}$ denotes the Gaussian free field on ${G}$ .

GFF on the 2D lattice; courtesy of Scott Sheffield.

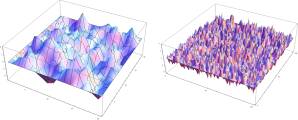
Here ${A \asymp B}$ is the assertion that ${A}$ and ${B}$ are within universal constant factors. In particular, we use this theorem to give a deterministic ${O(1)}$ -approximation to the cover time, answering a question of Aldous and Fill, and to resolve the Winkler-Zuckerman blanket time conjectures.
This follows some partial progress on these questions by Kahn, Kim, Lovasz, and Vu (1999).

2. Derandomizing the cover time

The cover time is one of the few basic graph parameters which can easily be computed by a randomized polynomial-time algorithm, but for which we don’t know of a deterministic counterpart. More precisely, for every ${\varepsilon > 0}$ , we can compute a ${(1+\varepsilon)}$ -approximation to the cover time by simulating the random walk enough times and taking the median estimate, but even given the above results, the best we can do in deterministic polynomial-time is an ${O(1)}$ -approximation.

We now describe one conjectural path to a better derandomization. Let ${t_{\mathrm{hit}}(G) = \max_{u,v \in V} H(u,v)}$ denote the maximal hitting time in ${G}$ , where ${H(u,v)}$ is the expected number of steps needed to hit ${v}$ from a random walk started at ${u}$ . We prove the following more precise estimate.

Theorem 2 There is a constant ${C > 0}$ such that for every graph ${G=(V,E)}$ ,

$\displaystyle t_{\mathrm{cov}}(G) \leq \left(1+C\sqrt{\frac{t_{\mathrm{hit}}(G)}{t_{\mathrm{cov}}(G)}}\right) |E| \left(\mathop{\mathbb E} \max_{v \in V} g_v\right)^2.$

This prompts the following conjecture, which describes a potentially deeper connection between cover times and the GFF.

Conjecture 1 For a sequence of graphs ${\{G_n=(V_n,E_n)\}}$ with ${t_{\mathrm{hit}}(G_n) = o(t_{\mathrm{cov}}(G_n))}$ ,

$\displaystyle t_{\mathrm{cov}}(G_n) \sim |E_n| \left(\mathop{\mathbb E} \max_{v\in V_n} g^{(n)}_v\right)^2,$

where ${\{g^{(n)}_v\}}$ denotes the GFF on ${G_n}$ .

Here, we use ${a_n \sim b_n}$ to denote ${\lim a_n/b_n = 1}$ . The conjecture holds in some interesting cases, including the complete graph, the discrete ${2D}$ torus, and complete ${d}$ -ary trees. (See the full paper for details; except for the complete graph, these exact estimates are entire papers in themselves.)

Since the proof of Theorem 1 makes heavy use of the Fernique-Talagrand majorizing measures theory for estimating ${\mathop{\mathbb E} \max_{v \in V} g_v}$ , and this theory is bound to lose a large multiplicative constant, it seems that new techniques will be needed in order to resolve the conjecture. In particular, using the isomorphism theory discussed below, it seems that understanding the structure of the near-maxima, i.e. those points ${g_v}$ which achieve ${g_v \geq (1-\varepsilon) \left(\mathop{\mathbb E} \max_{v \in V} g_v\right)}$ , will be an essential part of any study.

The second part of such a derandomization strategy is the ability to compute a deterministic ${(1+\varepsilon)}$ -approximation to ${\mathop{\mathbb E} \max_{v \in V} g_v}$ .

Question 1 For every ${\varepsilon > 0}$ , is there a deterministic polynomial-time algorithm that, given a finite set of points ${X \subseteq \mathbb R^n}$ , computes a ${(1+\varepsilon)}$ -approximation to the value

$\displaystyle \mathop{\mathbb E} \max_{x \in X} \langle g,x\rangle,$

where ${g}$ is a standard ${n}$ -dimensional Gaussian? Is this possible if we know that ${X}$ has the covariance structure of a Gaussian free field?

3. Understanding the Dynkin Isomorphism Theory

Besides majorizing measures, another major tool used in our work is the theory of isomorphisms between Markov processes and Gaussian processes. We now switch to considering the continuous-time random walk on a graph ${G}$ . This makes the same transitions as the simple discrete-time walk, but now spends an exponential (with mean one) amount of time at every vertex. We define the local time at ${v}$ at time ${t}$ by

$\displaystyle L_t^v = \frac{\textrm{amount of time spent at } v}{\mathrm{deg}(v)}$

when we have run the random walk for time ${t}$ .

Work of Ray and Knight in the 1960’s characterized the local times of Brownian motion, and then in 1980, Dynkin described a general connection between the local times of Markov processes and associated Gaussian processes. The version we use is due to Eisenbaum, Kaspi, Marcus, Rosen, and Shi (2000).

Theorem 3 Let ${G=(V,E)}$ and fix some ${v_0 \in V}$ , which is the origin of the random walk. Let ${\ell > 0}$ be given, and define the (random) time ${T=T(\ell)=\inf \{ t: L_t^{v_0} \geq \ell \}}$ . If ${\{g_v\}_{v \in V}}$ is the GFF with ${g_{v_0}=0}$ , then

$\displaystyle \left\{ L_T^x + \frac12 g_x^2 : x \in V \right\} \stackrel{\mathrm{law}}{=} \left\{ \frac12 (g_x - \sqrt{2\ell})^2 : x \in V\right\}.$

Note that on the left hand side, the local times ${\{L_T^x\}}$ and the GFF ${\{g_x\}}$ are independent. This remarkable theorem (and many others like it) are proved in the book of Marcus and Rosen. In the introduction, the authors describe the “wonderful, mysterious isomorphism theorems.” They continue,

Another confession we must make is that we do not really understand the actual relationship between local times… and their associated Gaussian processes. If one asks us, as is often the case during lectures, to give an intuitive description… we must answer that we cannot. We leave this extremely interesting question to you.

So I will now pass the question along. The proof of the isomorphism theorems proceeds by taking Laplace transforms and then doing some involved combinatorics. It’s analogous to the situation in enumerative combinatorics where we have a generating function proof of some equality, but not a bijective proof where you can really get your hands on what’s happening.

What is the simplest isomorphism-esque statement which has no intuitive proof? The following lemma is used in the proof of the original Ray-Knight theorem on Brownian motion (see Lemma 6.32 in the Morters-Peres book). It can be proved in a few lines using Laplace transforms, yet one suspects there should be an explicit coupling.

Lemma 4 For any ${\ell > 0}$ , the following holds. Suppose that ${X}$ is a standard normal, ${Z_1, Z_2, \ldots}$ are i.i.d. standard exponentials, and ${N}$ is Poisson with parameter ${\ell^2/2}$ . If all these random variables are independent, then

$\displaystyle (X+\ell)^2 \stackrel{\mathrm{law}}{=} X^2 + 2 \sum_{j=1}^N Z_j.$

Amazing! The last open question is to explain this equality of distributions in a satisfactory manner, as a first step to understanding what’s really going on in the isomorphism theory.

5 thoughts on “Open question: Cover times and the Gaussian free field”

aram says:

December 10, 2010 at 7:05 am

Those are really interesting questions!

For question 1, how much do things change if is replaced by ^2?
i.e. is it still open? still interesting?

Also, in your third equation in section 1, I think you want a 1/R_eff(u,v) in the exponent.
James Lee says:

December 10, 2010 at 3:44 pm

Hi Aram,

I think your first question didn’t come through correctly.

Also, there is no 1/R_eff(u,v) in that equation. The effective resistance comes out naturally from the fact that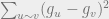 $\sum_{u \sim v} (g_u - g_v)^2$ is the quadratic form arising from the Laplacian.
James Lee says:

December 11, 2010 at 12:47 pm

Aram’s first question is about a deterministic approximation to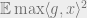 $\mathbb{E} \max \langle g,x\rangle^2$ in Question 1, vs. $\mathbb{E} \max \langle g,x\rangle$ . Good question.

In the regime where $\max_{x \in X} \mathbb{E} (g_x^2) = o(\mathbb{E} \max_{x \in X} g_x^2)$ , by concentration properties of Gaussians, we have

$\displaystyle \left(\mathbb{E} \max_{x \in X} g_x\right)^2 \sim \mathbb{E} \max_{x \in X} g_x^2,$

so the two questions are the same. For the GFF, this corresponds to the regime in which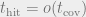 $t_{\mathrm{hit}} = o(t_{\mathrm{cov}})$ .

You’re right, it may be that approximating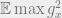 $\mathbb{E} \max g_x^2$ is more natural. But it seems that for the most interesting range of parameters, the questions coincide.
Pingback: Open question recap | tcs math - some mathematics of theoretical computer science
Pingback: Workshop on Chaining Methods (guest post by Jelani Nelson) | Windows On Theory