Lecture P1. From Integrality Gaps to Dictatorship Tests

Here are Prasad Raghavendra‘s notes on one of two guest lectures he gave for CSE 599S. Prasad will be a faculty member at Georgia Tech after he finishes his postdoc at MSR New England.

In yet another excursion in to applications of discrete harmonic analysis, we will now see an application of the invariance principle, to hardness of approximation. We will complement this discussion with the proof of the invariance principle in the next lecture.

1. Invariance Principle

In its simplest form, the central limit theorem asserts the following: “As ${n}$ increases, the sum of ${n}$ independent bernoulli random variables ( ${\pm 1}$ random variables) has approximately the same distribution as the sum of ${n}$ independent normal (Gaussian with mean ${0}$ and variance ${1}$ ) random variables”

Alternatively, as ${n}$ increases, the value of the polynomial ${F(\mathbf x) = \frac{1}{\sqrt{n}} (x^{(1)} + x^{(2)} + \ldots x^{(n)})}$ has approximately the same distribution whether the random variables ${x^{(i)}}$ are i.i.d Bernoulli random variables or i.i.d normal random variables. More generally, the distribution of ${p(\mathbf x)}$ is the approximately the same as long as the random variables ${x^{(i)}}$ are independent with mean ${0}$ , variance ${1}$ and satisfy certain mild regularity assumptions.

A phenomenon of this nature where the distribution of a function of random variables, depends solely on a small number of their moments is referred to as invariance.

A natural approach to generalize of the above stated central limit theorem, is to replace the “sum” ( ${\frac{1}{\sqrt{n}} (x^{(1)} + x^{(2)} + \ldots x^{(n)})}$ ) by other multivariate polynomials. As we will see in the next lecture, the invariance principle indeed holds for low degree multilinear polynomials that are not influenced heavily by any single coordinate. Formally, define the influence of a coordinate on a polynomial as follows:

Definition 1 For a multilinear polynomial ${F(\mathbf{x}) = \sum_{\sigma} \hat{F}_{\sigma} \prod_{i \in [R]} x^{(\sigma_i)}}$ define the influence of the ${i^{th}}$ coordinate as follows:

${ \mathrm{Inf}_{i}(F) = \mathop{\mathbb E}_{x} [\mathrm{Var}_{x^{(i)}}[F]] = \sum_{\sigma_{i} \neq 0} \hat{F}^2_\sigma}$

Here ${\mathrm{Var}_{x^{(i)}}[F]}$ denotes the variance of ${F(x)}$ over random choice of ${x_i}$ .

The invariance principle for low degree polynomials was first shown by Rotar in 1979. More recently, invariance principles for low degree polynomials were shown in different settings in the work of Mossel-O’Donnell-Olekszciewicz and Chatterjee. The former of the two works also showed the Majority is Stablest conjecture, and has been influential in introducing the powerful tool of invariance to hardness of approximation.

Here we state a special case of the invariance principle tailored to the application at hand. To this end, let us first define a rounding function ${f_{[-1,1]}}$ as follows:

$\displaystyle f_{[-1,1]}(x) = \begin{cases} -1 &\text{ if } x < -1 \\ x &\text{ if } -1\leqslant x\leqslant 1 \\ 1 &\text{ if } x > 1 \end{cases}$

Theorem 2 (Invariance Principle [Mossel-ODonnell-Oleszkiewicz]) Let ${\mathbf{z} = \{z_1, z_2\}}$ and ${\mathbf{G} = \{g_1,g_2\}}$ be sets of Bernoulli and Gaussian random variables respectively. Furthermore, let

$\displaystyle \mathop{\mathbb E}[z_i] = \mathop{\mathbb E}[g_i] = 0 \qquad \qquad \mathop{\mathbb E}[z_i^2] = \mathop{\mathbb E}[g_i^2] = 1 \qquad \qquad \forall i \in [2]$

and ${\mathop{\mathbb E}[z_1 z_2] = \mathop{\mathbb E}[g_1 g_2]}$ . Let ${\mathbf{z}^R, \mathbf{G}^R}$ denote ${R}$ independent copies of the random variables ${\mathbf{z}}$ and ${\mathbf{G}}$ .

Let ${F}$ be a multilinear polynomial given by ${F(\mathbf{x}) = \sum_{\sigma} \hat{F}_{\sigma} \prod_{i \in \sigma} x^{(i)}}$ , and let ${H(\mathbf{x})=T_{1-\epsilon} F(\mathbf{x}) = \sum_{\sigma}(1-\epsilon)^{|\sigma|} \hat{F}_{\sigma} \prod_{i\in \sigma} x^{(i)}}$ . If ${\mathrm{Inf}_\ell(H) \leqslant \tau}$ for all ${\ell \in [R]}$ , then the following statements hold:

For every function ${\Psi : \mathbb{R}^2 \rightarrow \mathbb{R}}$ which is thrice differentiable with all its partial derivatives up to order ${3}$ bounded uniformly by ${C_0}$ ,

$\displaystyle \Big|\mathop{\mathbb E}\Big[\Psi(H(\mathbf{z}_1^{R}), H(\mathbf{z}_2^{R}))\Big] - \mathop{\mathbb E}\Big[\Psi(H(\mathbf{g}_1^R), H(\mathbf{g}_2^R))\Big] \Big| \leqslant \tau^{O(\epsilon)}$

Define the function ${\xi : {\mathbb R}^2 \rightarrow {\mathbb R}}$ as ${\xi(\mathbf{x}) = \sum_{i\in [2]} (x_i - f_{[-1,1]}(x_i))^2}$ Then, we have ${ \Big|\mathop{\mathbb E}[\xi(H(\mathbf{z}_1^{n}), H(\mathbf{z}_2^{n}))] - \mathop{\mathbb E}[\xi(H(\mathbf{g}_1^{n}),H(\mathbf{g}_2^{n}))] \Big| \leqslant \tau^{O(\epsilon)} }$

2. Dictatorship Testing

A boolean function ${\mathcal{F}(x_1,x_2,\ldots,x_n)}$ on ${n}$ bits is a dictator or a long code if ${\mathcal{F}(x) = x_i}$ for some ${i}$ . Given the truth table of a function ${\mathcal{F}}$ , a dictatorship test is a randomized procedure that queries a few locations (say ${2}$ ) in the truth table of ${\mathcal{F}}$ , and tests a predicate ${P}$ on the values it queried. If the queried values satisfy the predicate ${P}$ , the test outputs ACCEPT else it outputs REJECT. The goal of the test is to determine if ${\mathcal{F}}$ is a dictator or is far from being a dictator. The main parameters of interest in a dictatorship test are :

Completeness ${(c)}$ Every dictator function ${\mathcal{F}(x) = x_i}$ is accepted with probability at least ${c}$ .
Soundness ${(s)}$ Any function ${\mathcal{F}}$ which is far from every dictator is accepted with probability at most ${s}$ .
Number of queries made, and the predicate ${P}$ used by the test.

2.1. Motivation

The motivation for the problem of dictatorship testing arises from hardness of approximation and PCP constructions. To show that an optimization problem ${\Lambda}$ is ${\mathbf{NP}}$ -hard to approximate, one constructs a reduction from a well-known ${\mathbf{NP}}$ -hard problem such as Label Cover to ${\Lambda}$ . Given an instance ${\Im}$ of the Label Cover problem, a hardness reduction produces an instance ${\Im'}$ of the problem ${\Lambda}$ . The instance ${\Im'}$ has a large optimum value if and only if ${\Im}$ has a high optimum. Dictatorship tests serve as “gadgets” that encode solutions to the Label Cover, as solutions to the problem ${\Lambda}$ . In fact, constructing an appropriate dictatorship test almost always translates in to a corresponding hardness result based on the Unique Games Conjecture.

Dictatorship tests or long code tests as they are also referred to, were originally conceived purely from the insight of error correcting codes. Let us suppose we are to encode a message that could take one of ${R}$ different values ${\{m_1,\ldots,m_{R}\}}$ . The long code encoding of the message ${m_\ell}$ is a bit string of length ${2^{R}}$ , consisting of the truth table of the function ${\mathcal{F}(x_1,\ldots,x_R) = x_\ell}$ . This encoding is maximally redundant in that any binary encoding with more than ${2^{R}}$ bits would contain ${2}$ bits that are identical for all $R$ messages. Intuitively, greater the redundancy in the encoding, the easier it is to perform the reduction.

While long code tests/dictatorship tests were originally conceived from a coding theoretic perspective, somewhat surprisingly these objects are intimately connected to semidefinite programs. This connection between semidefinite programs and dictatorship tests is the subject of today’s lecture. In particular, we will see a black-box reduction from SDP integrality gaps for Max Cut to dictatorship tests that can be used to show hardness of approximating Max Cut.

2.2. The case of Max Cut

The nature of dictatorship test needed for a hardness reduction varies with the specific problem one is trying to show is hard. To keep things concrete and simple, we will restrict our attention to the Max Cut problem.

A dictatorship test ${\mathsf{DICT}}$ for the Max Cut problem consists of a graph on the set of vertices ${\{\pm 1\}^{R}}$ . By convention, the graph ${\mathsf{DICT}}$ is a weighted graph where the edge weights form a probability distribution (sum up to ${1}$ ). We will write ${(\mathbf{z},\mathbf{z}') \in \mathsf{DICT}}$ to denote an edge sampled from the graph ${\mathsf{DICT}}$ (here ${\mathbf{z},\mathbf{z}' \in \{\pm 1\}^{R}}$ ).

A cut of the ${\mathsf{DICT}}$ graph can be thought of as a boolean function ${\mathcal{F} : \{\pm 1\}^R \rightarrow \{\pm 1\}}$ . For a boolean function ${\mathcal{F} : \{\pm 1\}^R \rightarrow \{\pm 1\}}$ , let ${\mathsf{DICT}(\mathcal{F})}$ denote the value of the cut. The value of a cut ${\mathcal{F}}$ is given by

$\displaystyle \mathsf{DICT}(\mathcal{F}) = \frac{1}{2}\mathop{\mathbb E}_{ (\mathbf{z}, \mathbf{z}')} \Big[ 1 - \mathcal{F}(\mathbf{z}) \mathcal{F}(\mathbf{z}') \Big]$

It is useful to define ${\mathsf{DICT}(\mathcal{F})}$ , for non-boolean functions ${\mathcal{F}: \{\pm 1\}^R \rightarrow [-1,1]}$ that take values in the interval ${[-1,1]}$ . To this end, we will interpret a value ${\mathcal{F}(\mathbf{z}) \in [-1,1]}$ as a random variable that takes ${\{\pm 1\}}$ values. Specifically, we think of a number ${a \in [-1,1]}$ as the following random variable

$ latex a = -1 $ with probability $\frac{1-a}{2}$ and $a = 1$ with probability $\frac{1+a}{2}$.

With this interpretation, the natural definition of ${\mathsf{DICT}(\mathcal{F})}$ is as follows:

$\displaystyle \mathsf{DICT}(\mathcal{F}) = \frac{1}{2}\mathop{\mathbb E}_{ (\mathbf{z}, \mathbf{z}') \in \mathsf{DICT}} \Big[ 1 - \mathcal{F}(\mathbf{z}) \mathcal{F}(\mathbf{z}') \Big] {\,.}$

Indeed, the above expression is equal to the expected value of the cut obtained by randomly rounding the values of the function ${\mathcal{F} : \{\pm 1\}^{R} \rightarrow [-1,1]}$ to ${\{\pm 1\}}$ as described in Equation 2.

The dictator cuts are given by the functions ${\mathcal{F}(\mathbf{z}) = z_\ell}$ for some ${\ell \in [R]}$ . The ${\mathsf{Completeness}}$ of the test ${\mathsf{DICT}}$ is the minimum value of a dictator cut, i.e.,

$\displaystyle \mathsf{Completeness}(\mathsf{DICT}) = \min_{\ell \in [R]} \mathsf{DICT}(z_{\ell})$

The soundness of the dictatorship test is the value of cuts that are far from every dictator. We will formalize the notion of being far from every dictator is formalized using influences as follows:

Definition 3 ( ${(\epsilon,\tau)}$ -quasirandom) A function ${\mathcal{F} : \{\pm 1\}^R \rightarrow [-1,1]}$ is said to be ${(\epsilon,\tau)}$ -quasirandom if for all ${\ell \in [R]}$ , ${\mathrm{Inf}_{\ell}(T_{1-\epsilon}\mathcal{F}) \leq \tau}$ .

Definition 4 ( ${\mathsf{Soundness}_{\epsilon,\tau}}$ ) For a dictatorship test ${\mathsf{DICT}}$ over ${\{\pm 1\}^{R}}$ and ${\epsilon, \tau > 0}$ , define the soundness of ${\mathsf{DICT}}$ as

$\displaystyle \mathsf{Soundness}_{\epsilon,\tau}(\mathsf{DICT}) = \sup_{\mathcal{F} \text{ is } (\epsilon,\tau)-\text{quasirandom}} \mathsf{DICT}(\mathcal{F})$

2.3. SDP Relaxation

Let ${G = (V,E)}$ be an an instance of the Max Cut problem. Specifically, ${G}$ is a weighted graph over a set of vertices ${V = \{v_1, \ldots, v_n\}}$ , whose edge weights sum up to ${1}$ (by convention). Thus, the set of edges ${E}$ will also be thought of as a probability distribution over edges. Let us the Goemans-Williamson semidefinite programming relaxation for Max Cut. The variables of the GW SDP consist of a set of vectors ${\mathbf V = \{ \mathbf v_1, \ldots,\mathbf v_n\}}$ , one vector for each vertex in the graph ${G}$ .

GW SDP Relaxation
Maximize $\mathrm{val}(\mathbf V) = \frac{1}{2}\mathop{\mathbb E}_{(v_i,v_j) \in E} \Big[ 1-\langle{\mathbf v_i, \mathbf v_j}\rangle \Big]$ (Average Squared Length of Edges)

Subject to $\lVert \mathbf v_i\rVert_2^2 = 1 \qquad \forall i, 1 \leqslant i \leqslant n$ (all vectors $\latex \mathbf v_i\ $ are unit vectors)

3. Intuition

Let ${G = (V,E)}$ be an an arbitrary instance of the Max Cut problem and let ${\mathbf V}$ denote a feasible solution to the GW SDP relaxation. We begin by presenting the intuition behind the black box reduction.

3.1. Dimension Reduction

Without loss of generality, the SDP solution ${\mathbf V}$ can be assumed to lie in a large constant dimensional space. Specifically, given an arbitrary SDP solution ${\mathbf V}$ in ${n}$ -dimensional space, project it in to a random subspace of dimension ${R}$ – a large constant. Random projections approximately preserve the lengths of vectors and distances between them. Hence, roughly speaking, the vectors produced after random projection yield a low-dimensional SDP solution to the same graph ${G}$ .

Formally, sample ${R}$ random Gaussian vectors ${\{ \mathbf \zeta_1 , \ldots, \mathbf \zeta_R \}}$ of the same dimension as the SDP vectors ${\mathbf V = \{ \mathbf v_1, \ldots, \mathbf v_n\}}$ . Here ${R}$ is to be thought of as a large constant independent of the size of the graph ${G}$ . Define a solution to the GW SDP relaxation as follows:

$\displaystyle \mathbf w_i = \frac{1}{\sqrt{\sum_{j \in [R]} {\langle{ \mathbf v_i, \mathbf \zeta_j} \rangle}^2}} \Big( \langle{\mathbf v_i, \mathbf \zeta_1}\rangle\ldots\langle{\mathbf v_i, \mathbf \zeta_R}\rangle\Big)$ for all vertices $v_i$ in graph $latex G$

The vector ${\mathbf w_i}$ is just the projection of the vector ${\mathbf v_i}$ along directions ${\{\mathbf \zeta_1, \ldots, \mathbf \zeta_R\}}$ , normalized to unit length. Clearly, the vectors ${\mathbf w_i}$ form a feasible SDP solution to GW SDP.

For every ${\eta > 0}$ , by choosing ${R}$ to be a sufficiently large constant, the following can be ensured: the distance between any two vectors ${\mathbf v_i}$ and ${\mathbf v_j}$ is preserved up to ${(1 \pm \epsilon)}$ -multiplicative factor with probability at least ${1-\epsilon}$ . Therefore, there exists some choice of ${\{ \mathbf \zeta_1, \ldots, \mathbf \zeta_R\}}$ such that the vectors ${\mathbf w_i}$ form a low dimensional SDP solution with roughly the same value as ${\{\mathbf v_i\}}$ , i.e., ${ \mathrm{val}(\{\mathbf w_1, \ldots, \mathbf w_n\}) \geqslant \mathrm{val}(\mathbf V) - \eta}$ . Henceforth, without loss of generality, let us assume that the SDP solution ${\mathbf V = \{ \mathbf v_1, \ldots, \mathbf v_n\}}$ consist of ${R}$ -dimensional vectors for a large enough constant ${R}$ .

3.2. Sphere Graph

A graph on the unit sphere, will consist of a set of unit vectors, and weigthed edges between them. As usual, the weights of the graph form a probability distribution, in that they sum up to ${1}$ .

The SDP solution ${\mathbf V}$ for a graph ${G}$ , yields a graph on the ${R}$ -dimensional unit sphere, which is isomorphic to ${G}$ . Recall that the objective value of the GW SDP is the average squared length of the edges. Hence, the SDP value remains unchanged under the following transformations:

Rotation Any rotation of the SDP vectors ${\mathbf V}$ about the origin, preserves the lengths of edges, and the distances between them. Thus, rotating the SDP solution ${\mathbf V}$ yields another feasible solution with the same objective value.
Union of Rotations Let ${\{ T_1 \mathbf v_1,\ldots, T_1 \mathbf v_n \}}$ and ${\{T_2 \mathbf v_1, \ldots, T_2 \mathbf v_n \}}$ be two solutions obtained by applying rotations ${T_1,T_2}$ to the SDP vectors ${\mathbf V}$ . Let ${G_1, G_2}$ be the associated graphs on the unit sphere. Let ${G'}$ denote the union of the two graphs, i.e., ${G' = G_1 \cup G_2}$ . The set of all distinct vectors in ${T_1 \mathbf V \cup T_2 \mathbf V}$ are the vertices of ${G'}$ . The edge distribution of ${G'}$ is the average of the edge distributions of ${G_1}$ and ${G_2}$ .The average squared lengths of edges in both ${T_1 \mathbf V}$ and ${T_2 \mathbf V}$ are equal to ${\mathrm{val}(\mathbf V)}$ . Hence, the average squared edge length in ${G'}$ is also equal to ${\mathrm{val}(\mathbf V)}$ . Thus, taking the union of two rotations of a graph preserves the SDP value.

Define the sphere graph ${{\mathcal S}_{\mathbf V}}$ as follows:

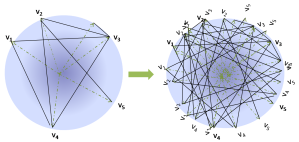
Sphere Graph ${{\mathcal S}_{\mathbf V}}$ : Union of all possible rotations of the graph ${G}$ (on the set of vectors ${\{\mathbf v_i\}}$ ) on the ${R}$ -dimensional unit sphere.

Clearly the sphere graph ${{\mathcal S}_{\mathbf V}}$ is an infinite graph. The sphere graph ${{\mathcal S}_{\mathbf V}}$ is solely a conceptual tool, and an explicit representation is never needed in the reduction. Nevertheless, due to its symmetry, indeed the sphere graph ${{\mathcal S}_{\mathbf V}}$ can be represented succinctly. By construction, the SDP value of the sphere graph ${{\mathcal S}_{\mathbf V}}$ is the same as that of the original graph ${G}$ . However, we will argue that ${{\mathcal S}_{\mathbf V}}$ is a harder instance of Max Cut than the original graph ${G}$ . In fact, given a cut for the sphere graph ${{\mathcal S}_{\mathbf V}}$ , it is possible to retrieve a cut for the original graph ${G}$ with the same objective value. Let us suppose ${\mathcal{F} : {\mathcal S}_{\mathbf V} \rightarrow \{\pm 1\}}$ is a cut of the sphere graph ${{\mathcal S}_{\mathbf V}}$ that cuts a ${c}$ -fraction of the edges. Notice that ${{\mathcal S}_{\mathbf V}}$ consists of a union of infinitely many copies (or rotations) of the graph ${G}$ . Therefore, on at least one of the copies of ${G}$ , the cut ${\mathcal{F}}$ must cut a ${c}$ -fraction of the edges. Indeed, if we have oracle access to the cut function ${\mathcal{F}}$ , we can efficiently construct a cut of the graph ${G}$ with the same value as ${\mathcal{F}}$ using the following rounding procedure:

${\mathsf{Round}_{\mathcal{F}}}$

Sample a rotation ${T}$ of the unit sphere, uniformly at random.

Output the cut induced by ${\mathcal{F} : {\mathcal S}_{\mathbf V} \rightarrow \{\pm 1\}}$ on the copy ${T \mathbf V}$ of the graph ${G}$ .

The expected value of the cut output by the ${\mathsf{Round}_{\mathcal{F}}}$ procedure is equal to the value of the cut ${\mathcal{F}}$ on the sphere graph ${{\mathcal S}_{\mathbf V}}$ . An immediate consequence is that,

$\displaystyle \mathrm{opt}({\mathcal S}_{\mathbf V}) \leqslant \mathrm{opt}(G) {\,.} \ \ \ \ \ (1)$

The sphere graph ${{\mathcal S}_{\mathbf V}}$ inherits the same SDP value as ${G}$ , while the optimum value ${\mathrm{opt}({\mathcal S}_{\mathbf V})}$ is at most that of the graph ${G}$ . In this light, the sphere graph ${{\mathcal S}_{\mathbf V}}$ is a harder instance of Max Cut than the original graph ${G}$ .

It is easy to see that the following is an equivalent definition for the sphere graph ${{\mathcal S}_{\mathbf V}}$ .

Definition 5 (Sphere Graph ${{\mathcal S}_{\mathbf V}}$ ) The set of vertices of ${{\mathcal S}_{\mathbf V}}$ is the set of all points on the ${R}$ -dimensional unit sphere. To sample an edge of ${{\mathcal S}_{\mathbf V}}$ use the following procedure,

Sample an edge ${(v_i, v_j)}$ in the graph ${G}$ ,

Sample two points ${(\mathbf{g},\mathbf{g}')}$ on the sphere at a squared distance ${\lVert{\mathbf v_i - \mathbf v_j}\rVert_2^2}$ uniformly at random.

Output the edge between ${(\mathbf{g}, \mathbf{g}')}$ .

3.3. Hypercube Graph

Finally, we are ready to describe the construction of the graph ${\mathsf{DICT}_{\mathbf{V}}}$ on the ${R}$ -dimensional hypercube. Here we refer to the hypercube suitably normalized to make all its points lie on the unit sphere.

${\mathsf{DICT}_{\mathbf{V}}}$

The set of vertices of ${\mathsf{DICT}_{\mathbf{V}}}$ are points in ${ \Big\{-\frac{1}{\sqrt{R}}, \frac{1}{\sqrt{R}}\Big\}^R}$ . An edge of ${\mathsf{DICT}_{\mathbf{V}}}$ can be sampled as follows:

Sample an edge ${(v_i, v_j)}$ in the graph ${G}$ .

Sample two points ${(\mathbf{z},\mathbf{z}')}$ in ${\{-\frac{1}{\sqrt{R}}, \frac{1}{\sqrt{R}} \}^{R}}$ , at squared distance ${\lVert{\mathbf v_i - \mathbf v_j}\rVert_2^2}$ uniformly at random.

Output the edge between ${(\mathbf{z}, \mathbf{z}')}$ .

It is likely that there are no pair of points on the hypercube ${ \Big\{-\frac{1}{\sqrt{R}}, \frac{1}{\sqrt{R}}\Big\}^R}$ at a distance exactly equal to ${\lVert{\mathbf v_i - \mathbf v_j}\rVert_2^2}$ . For the sake of exposition, let us ignore this issue for now. To remedy this issue, in the final construction, for each edge ${(v_i, v_j)}$ just introduce a probability distribution over edges such that the expected length of an edge is indeed ${\lVert{\mathbf v_i - \mathbf v_j}\rVert_2^2}$ .

Completeness:

Consider the ${\ell}$ th dictator cut ${\mathcal{F} : \mathsf{DICT}_{\mathbf{V}} \rightarrow \{\pm 1\}}$ given ${\mathcal{F}(\mathbf{z}) = \sqrt{R} z_\ell}$ . This corresponds to the axis-parallel cut of the ${\mathsf{DICT}_{\mathbf{V}}}$ graph along the ${\ell}$ th axis of the hypercube. Let us estimate the value of the cut ${\mathsf{DICT}_{\mathbf{V}}(\mathcal{F})}$ . An edge ${(\mathbf{z}, \mathbf{z}')}$ is cut by the ${\ell}$ th dictator cut if and only if ${z_\ell \neq z'_{\ell}}$ . Therefore, the value of the ${\ell}$ th dictator cut ${\mathcal{F}}$ is given by:

$\mathsf{DICT}_{\mathbf{V}}(\mathcal{F}) = \mathop{\mathbb E}_{(v_i, v_j) \in G} \mathop{\mathbb E}_{\mathbf{z},\mathbf{z}'} \Big[ \mathbf{1}[z_\ell\neq z'_\ell]\Big]$

Notice that two points ${\mathbf{z},\mathbf{z}'}$ at a squared distance ${\lVert{\mathbf{z}-\mathbf{z}'}\rVert_2^2}$ differ on exactly ${\frac{d}{4}}$ coordinates. Hence, two random points at distance ${\mathbf{z},\mathbf{z}'}$ at a squared distance ${\lVert{\mathbf{z}-\mathbf{z}'}\rVert_2^2 = d}$ differ on a given coordinate with probability ${\frac{d}{4}}$ . Therefore, let us rewrite the expression for ${\mathsf{DICT}_{\mathbf V}(\mathcal{F})}$ as follows:

$\displaystyle \mathsf{DICT}_{\mathbf V}(\mathcal{F})=\frac{1}{4}\mathop{\mathbb E}_{(v_i,v_j)\in G}\Big[\lVert{\mathbf v_i - \mathbf v_j}\rVert_2^2\Big]$

$\displaystyle=\frac{1}{2}\mathop{\mathbb{E}}_{(v_i, v_j) \in G}\Big[ 1 -\langle{\mathbf{v}_i, \mathbf{v}_j}\rangle\Big]=\mathrm{val}(\mathbf{V})$

Hence, ${\mathsf{Completeness}(\mathsf{DICT})}$ is at least ${\mathrm{val}(\mathbf V)}$ .

Soundness:

Consider a cut ${\mathcal{F} : \mathsf{DICT}_{\mathbf{V}} \rightarrow \{\pm 1\}}$ that is far from every dictator. Intuitively, the cut is not parallel to any of the axis of the hypercube. Note the strong similarity in the construction of the sphere graph ${{\mathcal S}_{\mathbf V}}$ and the hypercube graph ${\mathsf{DICT}_{\mathbf{V}}}$ . In both cases, we sampled two random points at a distance equal to the edge length. In fact, the hypercube graph ${\mathsf{DICT}_{\mathbf{V}}}$ is a subgraph of the sphere graph ${{\mathcal S}_{\mathbf V}}$ . The existence of special directions (the axis of the hypercube) is what distinguishes the hypercube graph ${\mathsf{DICT}_{\mathbf{V}}}$ from the sphere graph ${{\mathcal S}_{\mathbf V}}$ . Thus, roughly speaking, a cut ${\mathcal{F}}$ which is not paralel to any axis must be unable to distinguish between the sphere graph ${{\mathcal S}_{\mathbf V}}$ and the hypercube graph ${\mathsf{DICT}_{\mathbf{V}}}$ . If we visualize the cut ${\mathcal{F}}$ of ${\mathsf{DICT}_{\mathbf{V}}}$ as a geometric surface not parallel to any axis, then the same geometric surface viewed as a cut

Extending the cut from Hypercube to Sphere graph

of the sphere graph must separate roughly the same fraction of edges.

Indeed, the above intuition can be made precise if the cut ${\mathcal{F}}$ is sufficiently smooth (low degree). The cut ${\mathcal{F} : \mathsf{DICT}_{\mathbf{V}} \rightarrow \{\pm 1\}}$ can be expressed as a multilinear polynomial ${F}$ (by Fourier expansion), thus extending the cut function ${\mathcal{F}}$ from ${\{-\frac{1}{\sqrt{R}}, \frac{1}{\sqrt{R}}\}^{R}}$ to ${{\mathbb R}^{R}}$ . The function ${\mathcal{F}}$ is smooth if the corresponding polynomial polynomial ${F}$ is low degree. If ${\mathcal{F}}$ is smooth and far from every dictator, then one can show that,

$\displaystyle \text{ Value of } \mathcal{F} \text{ on } \mathsf{DICT}_{\mathbf{V}} \approx \text{ Value of } F \text{ on } {\mathcal S}_{\mathbf V}$

By Equation 1, the maximum value of a cut of the sphere graph ${{\mathcal S}_{\mathbf V}}$ is at most ${\mathrm{opt}(G)}$ . Therefore, for any cut ${\mathcal{F} : \mathsf{DICT}_{\mathbf{V}} \rightarrow \{\pm 1\}}$ that is smooth and far from every dictator, we get ${\mathsf{DICT}_{\mathbf{V}}(\mathcal{F}) \leqslant \mathrm{opt}(G)}$ .

Ignoring the smoothness condition for now, the above argument shows that the soundness of the dictatorship test ${\mathsf{DICT}_{\mathbf{V}}}$ is at most ${\mathrm{opt}(G)}$ . Summarizing the above discussion, starting from a SDP solution ${\{\mathbf v_i\}}$ for a graph ${G}$ , we constructed hypercube graph (dictatorship test) ${\mathsf{DICT}_{\mathbf{V}}}$ such that ${\mathsf{Completeness}(\mathsf{DICT}_{\mathbf{V}}) \geqslant \mathrm{val}(\{\mathbf v_i\})}$ , and ${\mathsf{Soundness}_{\epsilon,\tau} (\mathsf{DICT}_{\mathbf{V}}) \leqslant \mathrm{opt}(G)}$ .

By suitably modifying the construction of ${\mathsf{DICT}_{\mathbf{V}}}$ , the smoothness requirement for the cut can be dropped. The basic idea is fairly simple yet powerful. In the definition of ${\mathsf{DICT}_{\mathbf{V}}}$ , while introducing an edge between ${(\mathbf{z}, \mathbf{z}')}$ , perturb each coordinate of ${\mathbf{z}}$ and ${\mathbf{z}'}$ with a tiny probability ${\epsilon}$ to obtain ${\tilde{\mathbf{z}}}$ and ${\tilde{\mathbf{z}}'}$ respectively, then introduce the edge ${(\tilde{\mathbf{z}},\tilde{\mathbf{z}}')}$ instead of ${(\mathbf{z},\mathbf{z}')}$ . The introduction of noise to the vertices ${\mathbf{z}}$ and ${\mathbf{z}'}$ has an averaging effect on the cut function, thus making it smooth.

4. Formal Proof

Let ${G = (V,E)}$ be an arbitrary instance of Max Cut. Let ${\mathbf V = \{\mathbf v_1,\ldots,\mathbf v_n\}}$ be a feasible solution to the ${GW}$ SDP relaxation.

Locally, for every edge ${e = (v_i,v_j)}$ in ${G}$ , there exists a distribution over ${\{\pm 1\}}$ assignments that match the SDP inner products. In other words, there exists ${\{\pm 1\}}$ valued random variables ${z_i,z_j}$ such that

$\displaystyle \mathbf v_i \cdot \mathbf v_j = \mathop{\mathbb E}[z_i \cdot z_j]$

For each edge ${e = (v_i,v_j)}$ , let ${\mu_{e}}$ denote the local integral distribution over ${\{\pm 1\}}$ assignments.

The details of the construction of dictatorship test ${\mathsf{DICT}_{\mathbf V}}$ are as follows:

${\mathsf{DICT}_{\mathbf{V}}}$

The set of vertices of ${\mathsf{DICT}_{\mathbf V}}$ consist of the ${R}$ -dimensional hypercube ${\{\pm 1\}^{R}}$ . The distribution of edges in ${\mathsf{DICT}_{\mathbf V}}$ is the one induced by the following sampling procedure:

Sample an edge ${e = (v_i,v_j) \in E}$ in the graph ${G}$ .

Sample ${R}$ times independently from the distribution ${\mu_{e}}$ to obtain ${\mathbf{z}_i^R = (z_i^{(1)},\ldots, z_{i}^{(R)})}$ and ${\mathbf{z}^R_j = (z_j^{(1)},\ldots, z_{j}^{(R)})}$ , both in ${\{\pm 1\}^{R}}$ .

Perturb each coordinate of ${\mathbf{z}^R_i}$ and ${\mathbf{z}^R_j}$ independently with probability ${\epsilon}$ to obtain ${\tilde{\mathbf{z}}^R_i,\tilde{\mathbf{z}}^R_j}$ respectively. Formally, for each ${\ell \in [R]}$ ,
$\displaystyle \tilde{z}_i^{(\ell)} = \begin{cases} z_{i}^{(\ell)} & \text{ with probability } 1-\epsilon \\ \text{ uniformly random value in } \{\pm 1\} & \text{ with probability } \epsilon \end{cases}$

Output the edge ${(\tilde{\mathbf{z}}^{R}_i, \tilde{\mathbf{z}}^{R}_j)}$ .

Theorem 6 There exists absolute constants ${C,K}$ such that for all ${\epsilon, \tau \in [0,1]}$ , for any graph ${G}$ and an SDP solution ${\mathbf V = \{ \mathbf v_1, \ldots, \mathbf v_n\}}$ for the GW-SDP relaxation of ${G}$ ,

${\mathsf{Completeness}(\mathsf{DICT}_{\mathbf V}) \geqslant \mathrm{val}(\mathbf V) - 2\epsilon}$

${\mathsf{Soundness}_{\epsilon,\tau}(\mathsf{DICT}_{\mathbf V}) \leqslant \mathrm{opt}(G)+ C\tau^{K\epsilon}}$

Let ${\mathcal{F} : \{\pm 1\}^R \rightarrow \{\pm 1\}}$ be a cut of the ${\mathsf{DICT}}$ graph. The fraction of edges cut by ${\mathcal{F}}$ is given by

$\displaystyle \mathsf{DICT}_{\mathbf V}(\mathcal{F})=\frac{1}{2}\mathop{\mathbb E}_{(v_i,v_j) \in E} \mathop{\mathbb E}_{\mathbf{z}^R_{i}, \mathbf{z}^R_j}\mathop{\mathbb E}_{\tilde{\mathbf{z}}_i^R, \tilde{\mathbf{z}}_j^R}\Big[1-\mathcal{F}(\tilde{\mathbf{z}}_i^R) \cdot \mathcal{F}(\tilde{\mathbf{z}}_j^R)\Big]$

4.1. Completeness

Consider the ${\ell}$ th dictator cut given by ${\mathcal{F}(\mathbf{z}^R) = z^{(\ell)}}$ . With probability ${(1-\epsilon)^2}$ , the perturbation does not affect the ${\ell}$ th coordinate of ${\mathbf{z}_i}$ and ${\mathbf{z}_j}$ . In other words, with probability ${(1-\epsilon)^2}$ , the following hold: ${\tilde{z}^{(\ell)}_j =z^{(\ell)}_j}$ and ${\tilde{z}^{(\ell)}_i = z^{(\ell)}_i}$ . Hence,

$\displaystyle \mathsf{DICT}_{\mathbf V}(\mathcal{F}) \geqslant (1-\epsilon)^2 \cdot \frac{1}{2}\mathop{\mathbb E}_{e} \mathop{\mathbb E}_{\mathbf{z}^R_{i}, \mathbf{z}^R_j} \Big[1 - {z}_i^{(\ell)} \cdot {z}_j^{(\ell)}\Big]$

Observe that if the edge ${e = (v_i,v_j)}$ in ${G}$ is sampled, then the distribution ${\mu_{e}}$ is used to generate each coordinates of ${\mathbf{z}^{R}_i}$ and ${\mathbf{z}^{R}_j}$ . Specifically, this means that the coordinates ${z_i^{(\ell)}}$ and ${z_j^{(\ell)}}$ satisfy,

$\displaystyle \mathop{\mathbb E}_{\mathbf{z}_i^R, \mathbf{z}_j^R} \Big[ 1 - z_i^{(\ell)} \cdot z_j^{(\ell)}\Big] = \mathop{\mathbb E}_{\mu_e} [1-z_i^{(\ell)} \cdot z_j^{(\ell)}] = 1 - \langle{ \mathbf v_i , \mathbf v_j}\rangle {\,.}$

Therefore, ${ \mathsf{DICT}_{\mathbf V}(\mathcal{F}) \geqslant (1-\epsilon)^2 \cdot \frac{1}{2}\mathop{\mathbb E}_{e} \left[1 - \langle{ \mathbf v_i ,\mathbf v_j}\rangle\right] \geqslant (1-\epsilon)^2 \cdot \mathrm{val}(\mathbf V)}$ .

4.2. Soundness

For the sake of analysis, let us construct a graph ${{\mathcal G}_{\mathbf V}}$ , roughly similar to the sphere graph ${{\mathcal S}_{\mathbf V}}$ described earlier. Gaussian Graph ${{\mathcal G}_{\mathbf V}}$

The vertices of ${{\mathcal G}_{\mathbf V}}$ are points in ${{\mathbb R}^{R}}$ . The graph ${{\mathcal G}_{\mathbf V}}$ is the union of all random projections of the SDP solution ${\mathbf V}$ in to ${R}$ dimensions. Formally, an edge of ${{\mathcal G}_{\mathbf V}}$ can be sampled as follows:

Sample ${R}$ random Gaussian vectors ${\mathbf \zeta^{(1)}, \ldots, \mathbf \zeta^{(R)}}$ of the same dimension as the SDP solution ${\mathbf V}$ .

Project the SDP vectors ${\mathbf V =\{ \mathbf v_1,\ldots, \mathbf v_n\}}$ along directions ${\mathbf \zeta^{(1)}, \ldots,\mathbf \zeta^{(R)}}$ to obtain a copy of ${G}$ in a ${{\mathbb R}^{R}}$ . Formally define,
$\displaystyle \mathbf{g}_i^{R} = ( \langle{\mathbf v_i, \mathbf \zeta^{(1)}}\rangle, \ldots, \langle{\mathbf v_i,\mathbf \zeta^{(R)}}\rangle)$

Sample an edge ${e = (v_i, v_j)}$ in ${G}$ , and output the corresponding edge ${(\mathbf{g}_i^R,\mathbf{g}_j^R)}$ in ${{\mathbb R}^{R}}$

As lengths of vectors are approximately preserved under random projections, most of the vectors are ${\{\mathbf{g}_i^R\}}$ are roughly unit vectors. Hence, the Gaussian graph ${{\mathcal G}_{\mathbf V}}$ is a slightly fudged version of the sphere graph ${{\mathcal S}_{\mathbf V}}$ described earlier.

As the graph ${{\mathcal G}_{\mathbf V}}$ consists of a union of several isomorphic copies of ${G}$ , the following claim is an immediate consequence.

Claim 1 ${\mathrm{opt}({\mathcal G}_{\mathbf V}) \leqslant \mathrm{opt}(G)}$

Let us suppose ${\mathcal{F} : \{\pm 1\}^R \rightarrow \{\pm 1\}}$ be a ${(\tau,\epsilon)}$ -quasirandom function. For the sake of succinctness, let us denote ${\mathcal{H}= T_{1-\epsilon} \mathcal{F}}$ . Essentially, ${\mathcal{H}(\mathbf{z}^R)}$ is the expected value returned by ${\mathcal{F}}$ on querying a perturbation of the input ${\mathbf{z}^R}$ . Thus the function ${\mathcal{H}}$ is a smooth version of ${\mathcal{F}}$ , obtained by averaging the values of ${\mathcal{F}}$ .

Now we will extend the cut ${\mathcal{F}}$ from the hypercube graph ${\mathsf{DICT}_{\mathbf V}}$ to the Gaussian graph ${{\mathcal G}_{\mathbf V}}$ . To this end, write the functions ${\mathcal{H},\mathcal{F}}$ as written as a multilinear polynomials in the coordinates of ${\mathbf{z}^R = (z^{(1)},\ldots,z^{(R)})}$ . In particular, the Fourier expansion of ${\mathcal{F}}$ and ${\mathcal{H}}$ yields the intended multilinear polynomials.

$\displaystyle F(\mathbf{x}) = \sum_{\sigma} \hat{\mathcal{F}}_{\sigma} \prod_{i \in \sigma} x^{(i)} \qquad H(\mathbf{x}) = \sum_{\sigma} (1-\epsilon)^{|\sigma|} \hat{\mathcal{F}}_{\sigma} \prod_{i \in \sigma} x^{(i)}$

The polynomials ${F}$ and ${H}$ yield natural extension of the cut functions ${\mathcal{F}}$ and ${\mathcal{H}}$ from ${\{\pm 1\}^R}$ to ${{\mathbb R}^{R}}$ . However, unlike the original cut function ${\mathcal{F}}$ , the range of its extension need not be restricted to ${\{\pm 1\}}$ . To ensure that the extension defines a cut of the graph ${{\mathcal G}_{\mathbf V}}$ , let us round the extension in the most natural fashion using $f_{[-1,1]}$ . Specifically, the extension ${H^*}$ of the cut ${\mathcal{F}}$ to ${{\mathcal G}_{\mathbf V}}$ is given by

$\displaystyle H^{*}(\mathbf{g}^{R}) = f_{[-1,1]}(H(\mathbf{g}^{R}))$ where $\displaystyle H(\mathbf{g}^R) = \sum_{\sigma} (1-\epsilon)^{|\sigma|} \hat{\mathcal{F}_{\sigma}} \prod_{j \in \sigma} g^{(j)}$

Let ${\mathrm{val}(H^*)}$ denote the value of the cut ${H^*}$ of the graph ${{\mathcal G}_{\mathbf V}}$ . Now we can show the following claim.

Claim 2 For a ${(\tau,\epsilon)}$ -quasirandom function ${\mathcal{F} : \{\pm 1\}^{R} \rightarrow \{\pm 1\}}$ ,

$\displaystyle \mathrm{val}(H^*) = \mathsf{DICT}_{\mathbf V}(\mathcal{F}) \pm \tau^{O(\epsilon)}$

By definition of ${\mathrm{opt}({\mathcal G}_{\mathbf V})}$ , we have ${\mathrm{val}(H^*) \leqslant opt({\mathcal G}_{\mathbf V})}$ . Along with Claim 1, this implies that ${\mathsf{Soundness}_{\tau,\epsilon}(\mathsf{DICT}_{\mathbf V}) \leqslant \mathrm{opt}(G) + \tau^{O(\epsilon)}}$ , completing the proof of Theorem 6.

Proof: [Proof of Claim 2] Returning to the definition of ${\mathsf{DICT}_{\mathbf V}}$ , notice that the random variable ${\tilde{\mathbf{z}}_i^{R}}$ depends only on ${\mathbf{z}_i^{R}}$ . Thus, the value of a cut ${\mathcal{F} : \{\pm 1\}^R \rightarrow \{\pm 1\}}$ can be rewritten as,

$\displaystyle \mathsf{DICT}_{\mathbf V}(\mathcal{F}) = \frac{1}{2}\mathop{\mathbb E}_{e} \mathop{\mathbb E}_{\mathbf{z}^R_{i}, \mathbf{z}^R_j} \Big[ 1 - \mathop{\mathbb E}_{\tilde{\mathbf{z}}_i^R}[\mathcal{F}(\tilde{\mathbf{z}}_i^{R})| \mathbf{z}_i^{R}] \cdot \mathop{\mathbb E}_{\tilde{\mathbf{z}}_j^R}[\mathcal{F}(\tilde{\mathbf{z}}_j^R)| \mathbf{z}_j^{R}] \Big]$

By the definition of the noise operator ${T_{1-\epsilon}}$ , ${ T_{1-\epsilon} \mathcal{F}(\mathbf{z}^{R}) = \mathop{\mathbb E}_{\tilde{z}^R}[\mathcal{F}(\tilde{\mathbf{z}}^R)|\mathbf{z}^{R}] }$ . Hence ${\mathsf{DICT}_{\mathbf V}}$ can be rewritten as

$\displaystyle \mathsf{DICT}_{\mathbf V}(\mathcal{F}) = \frac{1}{2}\mathop{\mathbb E}_{e =(v_i,v_j)} \mathop{\mathbb E}_{\mathbf{z}^R_{i}, \mathbf{z}^R_j} \Big[ 1 - \mathcal{H}({\mathbf{z}}_i^{R}) \cdot \mathcal{H}({\mathbf{z}}_j^R)\Big] = \frac{1}{2}\mathop{\mathbb E}_{e=(v_i,v_j)} \mathop{\mathbb{E}}_{\mathbf{z}^R_{i}, \mathbf{z}^R_j} \Big[ 1 - H({\mathbf{z}}_i^{R}) \cdot H({\mathbf{z}}_j^R)\Big]$

By definition of the Gaussian graph ${{\mathcal G}_{\mathbf V}}$ , we have

$\displaystyle \mathrm{val}(H^*) = \frac{1}{2}\mathop{\mathbb E}_{e=(v_i,v_j)} \mathop{\mathbb E}_{\mathbf{g}^R_{i}, \mathbf{g}^R_j} \Big[ 1 - H^*({\mathbf{g}}_i^{R}) \cdot H^*({\mathbf{g}}_j^R)\Big]$

Firstly, let us denote by ${P : [-1,1]^2 \rightarrow [-1,1]}$ the function given by ${P(x,y) = 1-xy}$ . Let us restrict our attention to a particular edge ${e = (v_1,v_2)}$ . For this edge, we will show that

$\displaystyle \mathop{\mathbb E}_{\mathbf{z}_1^R, \mathbf{z}_2^R} \big[P(H(\mathbf{z}_1^R),H(\mathbf{z}_2^R))\big] = \mathop{\mathbb E}_{\mathbf{g}_1^R, \mathbf{g}_2^R} \big[P\left(H^*(\mathbf{g}_1^{R}),H^*(\mathbf{g}_2^{R})\right)\big] \pm \tau^{O(\epsilon)}$

By averaging the above equality over all edges ${e}$ in the graph ${G}$ , the claim follows. We will use the invariance principle to show the above claim.

By design, for each edge ${e = (v_i,v_j)}$ the pairs of random variables ${\{z_i,z_j\}}$ and ${\{g_i,g_j\}}$ satisfy,

$\displaystyle \mathop{\mathbb E}_{\mathbf \zeta}[g_i] = \mathop{\mathbb E}_{\mu_e}[z_i] = 0 \qquad \qquad \mathop{\mathbb E}_{\mathbf \zeta}[g_i^2] = \mathop{\mathbb E}_{\mu_e}[z_i^2] = 1$

$\displaystyle \mathop{\mathbb E}_{\mathbf \zeta}[g_j] = \mathop{\mathbb E}_{\mu_e}[z_j] = 0 \qquad \qquad \mathop{\mathbb E}_{\mathbf \zeta}[g_j^2] = \mathop{\mathbb E}_{\mu_e}[z_j^2] = 1$

$\displaystyle \qquad \mathop{\mathbb E}_{\mathbf \zeta}[g_i g_j] = \mathop{\mathbb E}_{\mu_e}[z_iz_j] = \langle{\mathbf v_i , \mathbf v_j}\rangle$

The predicate/payoff is currently defined as ${P(x,y) = 1-xy}$ in the domain ${[-1,1]^2}$ . Extend the payoff ${P}$ to a smooth function over the entire space ${\mathbb{R}^2}$ , with all its partial derivatives up to order ${3}$ bounded uniformly throughout ${\mathbb{R}^2}$ . Notice that the function ${P(x,y) = 1-xy}$ by itself does not have uniformly bounded derivatives in ${\mathbb{R}^2}$ . Further, it is easy to ensure that the extension satisfies the following Lipschitz condition for some large enough constant ${C > 0}$ ,

$\displaystyle |P(x,y) - P(x',y')| \leqslant C(|x-x'| + |y-y'|)$ for all $\displaystyle (x,y), (x',y') \in {\mathbb R}^2$

We will prove Equation 4 in two steps.

Step I : Apply the invariance principle with the ensembles ${\mathbf{z} = \{z_1,z_2\}}$ and ${\mathbf{G} = \{g_1,g_2\}}$ , for the vector of multilinear polynomials ${\mathbf{H}}$ and the smooth function ${\Psi = P}$ . This yields,

$\mathop{\mathbb E}_{\mathbf{z}^R_{1}, \mathbf{z}^R_2} \Big[ P(H(\mathbf{z}_1^R), H(\mathbf{z}_2^R))\Big] = \mathop{\mathbb E}_{\mathbf{g}^R_{1}, \mathbf{g}^R_2}\Big[ P(H(\mathbf{g}_1^R) , H(\mathbf{g}_2^R))\Big] \pm \tau^{O(\epsilon)}$

Step II : In this step, let us bound the effect of the rounding operation used in extending the cut ${\mathcal{F}}$ from ${\mathsf{DICT}_{\mathbf V}}$ to ${{\mathcal G}_{\mathbf V}}$ .

As ${\mathcal{F}}$ is a cut of ${\mathsf{DICT}_{\mathbf V}}$ , its range is ${\{\pm 1\}}$ . Hence, the corresponding polynomial ${F}$ takes ${\{\pm 1\}}$ values on inputs from ${\{\pm 1\}^R}$ . As ${H = T_{1-\epsilon} F}$ is an average of the values of ${F}$ , the values ${H(\mathbf{z}_1^R)}$ and ${H(\mathbf{z}_2^R)}$ are always in the range ${[-1,1]}$ .

By the invariance principle, the random variable ${(H(\mathbf{z}_1^{R}), H(\mathbf{z}_2^{R}))}$ has approximately the same behaviour as ${(H(\mathbf{g}_1^{R}), H(\mathbf{g}_2^R))}$ . Roughly speaking, this implies that the values ${H(\mathbf{g}_1^R), H(\mathbf{g}_2^R)}$ are also nearly always in the range ${[-1,1]}$ . Hence, intuitively the rounding operation must have little effect on the value of the cut.

This intuition is formalized by the second claim in the invariance principle. The function ${\xi}$ measures the squared deviation from the range ${[-1,1]}$ . For random variables ${(\mathbf{z}_1^{R}, \mathbf{z}_2^R)}$ , clearly we have ${\mathop{\mathbb E}[ \xi(H(\mathbf{z}_1^R), H(\mathbf{z}_2^R))] = 0}$ . By the invariance principle applied to polynomial ${H}$ we get,

$\displaystyle \mathop{\mathbb E}[\xi(H(\mathbf{g}_1^{n}),H(\mathbf{g}_2^{n}))] \leqslant \mathop{\mathbb E}[\xi(H(\mathbf{z}_1^{n}), H(\mathbf{z}_2^{n}))] + \tau^{O(\epsilon)} = 0 + \tau^{O(\epsilon)} = \tau^{O(\epsilon)} \ \ \ \ \ (2)$

Using the Lipschitz condition satisfied by the payoff,

$\displaystyle \Big|\mathop{\mathbb{E}}_{\mathbf{g}^{R}_1, \mathbf{g}^{R}_2}\big[ P(H^{*}(\mathbf{g}_1^R), H^{*}(\mathbf{g}_2^R))\big] - \mathop{\mathbb{E}}_{\mathbf{g}^R_{1},\mathbf{g}^R_2}\big[P(H(\mathbf{g}_1^R),H(\mathbf{g}_2^R))\big]\Big|$

$\displaystyle \leqslant C\mathop{\mathbb{E}}_{\mathbf{g}^{R}_1,\mathbf{g}^{R}_2}\Big[\big|H^{*}(\mathbf{g}_1^R)-H(\mathbf{g}_1^R)\big|+\big|H^{*}(\mathbf{g}_2^R)-H(\mathbf{g}_2^R)\big|\Big]$

$\displaystyle\leqslant C\Big( 2 \mathop{\mathbb{E}}_{\mathbf{g}^R_{1},\mathbf{g}^R_2}\Big[ \big|H^*(\mathbf{g}_1^R)-H(\mathbf{g}_1^R)\big|^2+\big|H^*(\mathbf{g}_2^R)-H(\mathbf{g}_2^R)\big|^2\Big]\Big)^{\frac{1}{2}}$ (By Cauchy Schwartz Inequality)

$\displaystyle\leqslant C\Big(2\mathop{\mathbb{E}}_{\mathbf{g}^R_{1},\mathbf{g}^R_2}\Big[\xi(H({\mathbf{g}}_1^R),H({\mathbf{g}}_2^R))\Big]\Big)^{\frac{1}{2}}$ (by definition of $\xi$ )

$\displaystyle \leqslant 2C\tau^{O(\epsilon)}$ (Equation 2)

Along with Equation 4, the above inequality implies Equation 4. This finishes the proof of Claim 2. $\Box$

5. Dictatorship Tests and Rounding Schemes

The soundness analysis can be translated in to an efficient rounding scheme. Specifically, given a cut ${\mathcal{F}}$ of the graph ${\mathsf{DICT}_{\mathbf V}}$ , let ${H^*}$ denote the extension of the cut to the Gaussian graph ${{\mathcal G}_{\mathbf V}}$ . The idea is to sample a random copy of the graph ${G}$ inside the Gaussian graph ${{\mathcal G}_{\mathbf V}}$ , and output the cut induced by ${H^*}$ on the copy. The details of the rounding scheme so obtained are as follows:

${\mathsf{Round}_{\mathcal{F}}}$

Input: SDP solution ${\mathbf V = \{\mathbf v_1, \ldots, \mathbf v_n\}}$ for the GW SDP relaxation of the graph ${G}$ .

Sample ${R}$ random Gaussian vectors ${\mathbf \zeta^{(1)}, \ldots, \mathbf \zeta^{(R)}}$ of the same dimension as the SDP solution ${\mathbf V}$ .

Project the SDP vectors ${\mathbf V =\{ \mathbf v_1,\ldots, \mathbf v_n\}}$ along directions ${\mathbf \zeta^{(1)}, \ldots,\mathbf \zeta^{(R)}}$ . Let
$\displaystyle\mathbf{g}_i^{R}=(\langle{\mathbf v_i,\mathbf \zeta^{(1)}}\rangle,\ldots,\langle{\mathbf v_i,\mathbf\zeta^{(R)}}\rangle)$

Compute ${H^*(\mathbf{g}^{R}_i)}$ for all ${i \in [n]}$ as $\displaystyle H^*(\mathbf{g}_i^{R})=f_{[-1,1]}H(\mathbf{g}_i^{R}))$ where $H(\mathbf{g}_i^R)=T_{1-\epsilon}F(\mathbf{g}_i^{R})=\sum_{\sigma} (1-\epsilon)^{|\sigma|}\hat{\mathcal{F}_{\sigma}}\prod_{j \in \sigma}g_i^{(j)}$

Assign vertex ${v_i}$ , the value ${1}$ with probability ${(1+H^*(\mathbf{g}^{R}_i))/2}$ and ${-1}$ with the remaining probability.

Let ${\mathsf{Round}_{\mathcal{F}}(\mathbf V)}$ denote the expected value of the cut returned by the above rounding scheme on an SDP solution ${\mathbf V}$ . Then,

$\displaystyle \mathsf{Round}_{\mathcal{F}}(\mathbf V) = \frac{1}{2}\mathop{\mathbb E}_{e=(v_i,v_j)} \mathop{\mathbb E}_{\mathbf{g}^R_{i}, \mathbf{g}^R_j} \Big[ 1 - H^*({\mathbf{g}}_i^{R}) \cdot H^*({\mathbf{g}}_j^R)\Big]$

The following is an immediate consequence of Claim 2,

Theorem 7 For a ${(\tau,\epsilon)}$ -quasirandom function ${\mathcal{F}: \{\pm 1\}^{R}\rightarrow \{\pm 1\}}$ ,

$\displaystyle \mathsf{Round}_{\mathcal{F}}(\mathbf V) = \mathsf{DICT}_{\mathbf V}(\mathcal{F})\pm \tau^{O(\epsilon)}$

The above theorem exposes an interesting duality between rounding schemes and dictatorship tests.

2 thoughts on “Lecture P1. From Integrality Gaps to Dictatorship Tests”

Punya says:

June 23, 2009 at 2:38 pm

What’s f_{[-1,1]} supposed to be in part 2 of the statement of Theorem 2?
Prasad says:

June 23, 2009 at 9:42 pm

Thanks! the definition of f_{[-1,1]} has been moved up from its earlier position to appear before Theorem 2.

f_{[-1,1]} is a function that is identity on the interval [-1,1] and truncates anything outside the interval to either -1 or 1 depending on its sign.

tcs math

some mathematics & computation

Lecture P1. From Integrality Gaps to Dictatorship Tests

Completeness:

Soundness:

2 thoughts on “Lecture P1. From Integrality Gaps to Dictatorship Tests”

Leave a comment

Completeness:

Soundness:

Share this:

Related

2 thoughts on “Lecture P1. From Integrality Gaps to Dictatorship Tests”

Leave a comment